Gotta Catch the Mode: What is the most average Pokémon?



Introduction (or Why?)
As part of my morning routine, I like to play Squirdle, one of many Wordle clones that requires you to guess some hidden value based on its properties. Wordle uses the position of letters, Worldle uses the shape of a country and its distance from your guesses, and Squirdle uses the attributes of Pokémon. The attributes used to guess the Pokémon are: Generation, Primary Type, Secondary Type, Height, and Weight.
Just like all other Wordle clones, Squirdle requires the player to make the first move. There are no hints to get you started, just a guess to be made, making your first move very important. In Wordle it is common to guess as many of the most common letters as possible. For example, my first guess is always 'steal', as it contains the two most common consonants and vowels ('s', 't', 'e', and 'a). Similarly, I use my knowledge of Pokémon to guess what I think is an average, and I always begin with Prinplup: It is a water type - one of the most common types - and lacks a secondary type, which eliminates a large portion of the Pokédex straight away. With a height of 0.8m (2'7") and a weight of 23kg (50.7lbs), Prinplup feels average, as (in my opinion) most Pokémon are designed to be friendly companions who can travel by your side. Finally, it was first released in Generation IV, making it roughly in the middle of the current nine generations of Pokémon.
However, all of these "deductions" are actually assumptions based on observations and half-remembered factoids from my time enjoying the franchise. Is Prinplup the ideal first guess? Does it eliminate enough of the Pokédex to be useful? And most importantly, does it actually help inform the following guesses? By interogating the data, we can hope to find answers to these questions by answering the following:
- What is the median generation?
- What is the most common type (and type combination)?
- What is the distribution of height across the Pokédex? and
- What is the distribution of weight?
Methodology
In order to answer these questions, I will be using Python (version 3), a simple but powerful programming language with great flexibility with regards to data manipulation and analysis. This is especially true once we include two key libraries: pandas and numpy. The former, pandas, allows us to open up data sets from spreadsheets and manipulate them using code. The latter, numpy, includes many tools for data manipulation. Finally I will be using matplotlib to represent the data graphically. All of this will be done in a Jupyter Notebook, allowing me to write explanations and observations next to the code and its results.
The data I am using was obtained from Pokémon Database's list of Pokémon stats which includes all of the information that I will need in order to answer the questions. It includes the different forms of a Pokémon, just like Squirdle, as well as all Pokémon from all DLC. I used Google Sheets to collect the data and export it as an Excel document for use with pandas.
import pandas import numpy import matplotlib.pyplot as plt pokemon_data = pandas.read_excel("PokemonData.xlsx", "Pokemon") print("Hello from Python!") pokemon_data
Hello from Python!
| Index | # | Name | Type | Height (ft) | Height (m) | Weight (lbs) | Weight (kgs) | BMI |
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | Bulbasaur | Grass\nPoison | 2′04″ | 0.7 | 15.2 | 6.9 | 14.1 |
| 1 | 2 | Ivysaur | Grass\nPoison | 3′03″ | 1.0 | 28.7 | 13.0 | 13.0 |
| 2 | 3 | Venusaur | Grass\nPoison | 6′07″ | 2.0 | 220.5 | 100.0 | 25.0 |
| 3 | 3 | Venusaur\nMega Venusaur | Grass\nPoison | 7′10″ | 2.4 | 342.8 | 155.5 | 27.0 |
| 4 | 4 | Charmander | Fire | 2′00″ | 0.6 | 18.7 | 8.5 | 23.6 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 1209 | 1023 | Iron Crown | Steel\nPsychic | 5′03″ | 1.6 | 343.9 | 156.0 | 60.9 |
| 1210 | 1024 | Terapagos\nNormal Form | Normal | 0′08″ | 0.2 | 14.3 | 6.5 | 162.5 |
| 1211 | 1024 | Terapagos\nTerastal Form | Normal | 1′00″ | 0.3 | 35.3 | 16.0 | 177.8 |
| 1212 | 1024 | Terapagos\nStellar Form | Normal | 5′07″ | 1.7 | 169.8 | 77.0 | 26.6 |
| 1213 | 1025 | Pecharunt | Poison\nGhost | 1′00″ | 0.3 | 0.7 | 0.3 | 3.3 |
What is the median generation?
As a demonstration of how the code will look and run, let's answer question 1: What is the median generation?
# List all current generations generations = list(range(1, 10)) # Calculate the median median = numpy.median(generations) # Display results print("Generations:", list(range(1,10))) print("Median:", median)
Generations: [1, 2, 3, 4, 5, 6, 7, 8, 9]
Median: 5.0
The range function takes two parameters, i and j, and generates an ordered array of numbers from i to j-1. list then converts that array to a list that can be read by numpy.median. As we can see, the answer to our first question is Generation V.
As I work on this, another question arises: Why are we finding the median generation? Could it be better to find the most populous generation? Each generation of the franchise introduces a different number of new Pokémon, so it could be considered beneficial to find the most populous generation and work outwards.
The number of generations is relatively small, especially when compared to the variation in height and weight. Additionally, the way Squirdle provides numerical clues (indicating greater than, less than, or equal to using arrows) makes it very easy for the player to mentally perform a binary search - for example, getting to Generation VI would take the route 5, 7, 6. The maximum number of guesses to find the correct generation with this method is 4 (i.e. to find Generation VIII: 5, 7, 9, 8), which only uses half of the eight total guesses the player has in each round of Squirdle. Therefore, I am deciding that the best information we can find is the median generation.
Analysis
Now that I have introduced my tools and answered my first question, it is time to turn to the data: 1214 rows constituting the 1025 current Pokémon in their different forms. Each question will be addressed separately, with its supporting code and data displayed.
What is the most common type (and type combination)?
This is perhaps the most important of the questions. As I mentioned above, it would be very easy to guess the generation of the Pokémon within the 8 guesses given to the player. The reverse is then true for the height and weight, with a huge range in what they can be, as seen below.
heights_m = pokemon_data["Height (m)"] heights_ft = pokemon_data["Height (ft)"] weights_kg = pokemon_data["Weight (kgs)"] weights_lbs = pokemon_data["Weight (lbs)"] print("Heights: %.1fm - %.1fm (%s - %s)" % \ (heights_m.min(), heights_m.max(), heights_ft.min(), heights_ft.max())) print("Weights: %.1fkg - %.1fkg (%slbs - %slbs)" % \ (weights_kg.min(), weights_kg.max(), weights_lbs.min(), weights_lbs.max()))
Heights: 0.1m - 20.0m (0′04″ - 9′10″)
Weights: 0.1kg - 999.9kg (0.2lbs - 2204.4lbs)
A range of 19.9m and 999.8kg makes it very difficult to arrive at the correct height and weight using binary search. The same is somewhat true for types. There are 18 types, and each Pokémon can have either a single type or a dual type. That means there are 18^2 (18 types times the 17 other types plus the option to have no secondary type) possible combinations. That's 324 possible type combinations! And with only 9 combinations that have never been used, there is no way to use binary search to find the correct combination in 8 guesses.
However, the player can guess 2 types in one go. So that is 324 possible combinations, minus the 9 unused combinations, and divided by 2, giving us roughly 158 guesses to find our type combination. Bare in mind that this does not account for standard type combinations that only tend to appear in a certain order, such as normal-flying, water-flying, or fire-fighting.
Using this information, I can see we need to find three pieces of information:
- How many mono-type Pokémon are there?
- What is the most common type overall?
- What is the most common type combination?
pokemon_data.head(8)
| Index | # | Name | Type | Height (ft) | Height (m) | Weight (lbs) | Weight (kgs) | BMI |
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | Bulbasaur | Grass\nPoison | 2′04″ | 0.7 | 15.2 | 6.9 | 14.1 |
| 1 | 2 | Ivysaur | Grass\nPoison | 3′03″ | 1.0 | 28.7 | 13.0 | 13.0 |
| 2 | 3 | Venusaur | Grass\nPoison | 6′07″ | 2.0 | 220.5 | 100.0 | 25.0 |
| 3 | 3 | Venusaur\nMega Venusaur | Grass\nPoison | 7′10″ | 2.4 | 342.8 | 155.5 | 27.0 |
| 4 | 4 | Charmander | Fire | 2′00″ | 0.6 | 18.7 | 8.5 | 23.6 |
| 5 | 5 | Charmeleon | Fire | 3′07″ | 1.1 | 41.9 | 19.0 | 15.7 |
| 6 | 6 | Charizard | Fire\nFlying | 5′07″ | 1.7 | 199.5 | 90.5 | 31.3 |
| 7 | 6 | Charizard\nMega Charizard X | Fire\nDragon | 5′07″ | 1.7 | 243.6 | 110.5 | 38.2 |
Looking at a sample of the data, we can see that Pokémon typing is all recorded in a single column. Whilst this makes the process of identifying mono-types slightly more difficult, there is a quick solution that does not require cleaning the data. Each entry in the Type field is either a single type (mono-type) or two types separated by a new line character (\n). This means I can filter the data set for entries where Type contains a new line character and get the length of the resulting set. This will tell us how many dual-type entries there are, meaning we can work out the number of mono-type entries.
dual_types = pokemon_data.loc[pokemon_data["Type"].str.contains('\n')] dual_type_count = dual_types.shape[0] total_pokemon = pokemon_data.shape[0] mono_type_count = total_pokemon - dual_type_count print("Total Pokémon: %i\nMono-Type Pokémon: %i (%.1f%%)\nDual-Type Pokémon: %i (%.1f%%)" % \ (total_pokemon, mono_type_count, 100*mono_type_count/total_pokemon, \ dual_type_count, 100*dual_type_count/total_pokemon))
Total Pokémon: 1214
Mono-Type Pokémon: 546 (45.0%)
Dual-Type Pokémon: 668 (55.0%)
Roughly half of all the entries represent a mono-type Pokémon, which currently suggests it does not matter much whether you guess a mono-type or dual-type first. However, in the search for the most average Pokémon, the slight bias toward dual-types might hold some influence. For now however I will focus on finding the next key piece of information: What is the most common type overall?
Whilst previously the use of \n wasn't much of an issue, it makes this next part more complicated. Rather than using a function built into pandas, I will need to write a small bit of code to split each entry in the Type field and collate the data. Luckily, this will not be an issue and should not take long to run.
types_count = {} def find_types(entry): types = entry.split('\n') for type in types: if type not in types_count.keys(): types_count[type] = 0 types_count[type] += 1 types_series = pokemon_data["Type"] types_series.map(find_types) types = pandas.DataFrame({'Type' : types_count.keys(), 'Count' : types_count.values()}) plot = types.sort_values(by="Count").plot.barh(x="Type", y="Count") plot.bar_label(plot.containers[0]) plot
<Axes: ylabel='Type'>
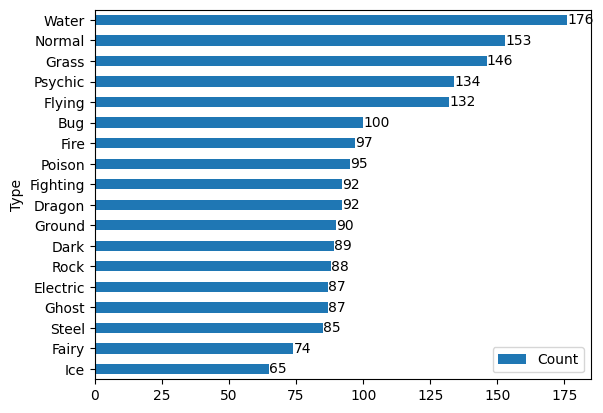
As can be seen on the plot of the data, water types are in fact the most common type by 23 points. Normal types come in second, with grass types coming in a close third. At the other end of the spectrum, ice types are the least common with only 65 entries, and fairy and steel types are only slightly ahead of them.
It makes sense that water types should be the most common, because - as with the real world - water covers much of the Pokémon world, with all regions having a costal region and a plethora of rivers, lakes, and ponds for the player to encounter. In fact, water has been an obstacle in every main-line Pokémon game in the franchise, which often follow a metroidvania-style lock and key system: The player needs to earn tools and moves that will help them navigate the world.
Guessing a water type first gives the best chance at guessing at least one of the two types of the Pokémon on your first guess. But once I've guessed a water-type, where should I go? If we introduce dual-types into this plot, what do we get?
all_combos = {} def find_all_types(entry): if entry not in all_combos.keys(): all_combos[entry] = 0 all_combos[entry] += 1 types_series.map(find_all_types) all_types = pandas.DataFrame({'Type' : all_combos.keys(), 'Count' : all_combos.values()}) print("Known Combinations: %i" % all_types.shape[0]) plotb = all_types.sort_values(by="Count").tail(15).plot.barh(x="Type", y="Count") plotb.bar_label(plotb.containers[0]) plotb
Known Combinations: 221
<Axes: ylabel='Type'>
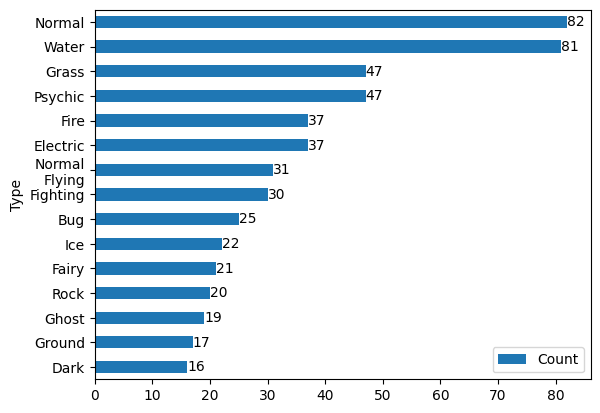
This graph shows the top 15 type combinations overall, and it goes a long way to show that - despite more than half of all Pokémon being dual-type - there are very few repeats of dual-type combinations, with a high concentration of Pokémon with specific single types. The only outlier seems to be normal-flying types, which occurs in every generation at least once, especially in early encounters (Pidgey and Spearow, Generation I and II; Taillow, Generation III; Starly, Generation IV; etc.). We can see that despite water being the most common type overall, normal types are the most common when dual-types are taken into consideration, but only by a single point.
More importantly, from this graph we can get our answers to the questions 'what is the most common type overall?' and 'what is the most common type combination?', the answers being normal types and normal-flying respectively. However it would also be useful to see the other common type combinations.
only_duals = all_types.loc[all_types["Type"].str.contains('\n')] plotc = only_duals.sort_values(by="Count").tail(10).plot.barh(x="Type", y="Count") plotc.bar_label(plotc.containers[0]) plotc
<Axes: ylabel='Type'>
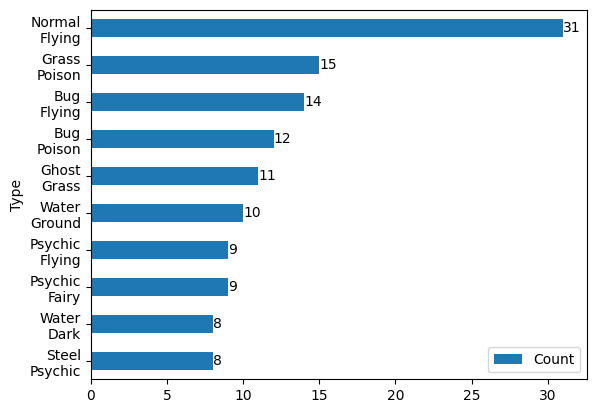
Here we can see the 10 most common type combinations, and we can see just how much of a lead normal-flying types have: 16 points! Grass-poison takes the second place slot, with bug-flying coming in a close third. Why do we need to know this? Despite knowing that water is the most common typing overall, normal being the most common mono-typing, and normal-flying the most common dual-typing, I realise that consideration is needed for the rules of the game. With 8 guesses before losing, it does not make sense to guess only mono-types. Therefore an additional question needs answering before we consider height and weight: how many guesses are needed to cover all type combinations?
def shortest_path(): seen_types = [] count = 1 for entry in only_duals.sort_values(by="Count", ascending=False)["Type"]: entry_types = entry.split('\n') if entry_types[0] in seen_types: continue if len(entry_types) > 1: if entry_types[1] in seen_types: continue seen_types += entry_types print(count, ' '.join(entry_types)) count += 1 shortest_path()
1 Normal Flying
2 Grass Poison
3 Water Ground
4 Psychic Fairy
5 Fire Fighting
6 Bug Steel
7 Dragon Ice
8 Rock Electric
9 Dark Ghost
These nine type combinations are, in order of commonality, the shortest route to guessing all types that a Pokémon could be. This list would look slightly different if I include the assumed first guess of a water type.
def shortest_path_no_water(): seen_types = ["Water"] count = 1 for entry in only_duals.sort_values(by="Count", ascending=False)["Type"]: entry_types = entry.split('\n') if entry_types[0] in seen_types: continue if len(entry_types) > 1: if entry_types[1] in seen_types: continue seen_types += entry_types print(count, ' '.join(entry_types)) count += 1 shortest_path_no_water()
1 Normal Flying
2 Grass Poison
3 Psychic Fairy
4 Dragon Ground
5 Fire Fighting
6 Bug Steel
7 Rock Electric
8 Dark Ice
This list is shorter, but we no longer guess ghost type, meaning that if Squirdle were based on type alone, it would be impossible to figure out the correct Pokémon in the 8 guesses provided. However, with the introduction of height and weight values, 8 guesses are more than enough.
What is the distribution of height across the Pokédex?
Based on what I have examined so far, the most average Pokémon - and therefore the best first guess in Squirdle - is a Generation V water type. According to Pokémon Database, that is a shortlist of 17 Pokémon, 7 if you exclude dual-types. How can we further narrow the search? Our first aspect to examine is height.
I will be looking at the distribution of height across all Pokémon, which can be best achieved via a box plot. I will only be performing this for metric weights, before converting the results to imperial units.
height_plot = pokemon_data.boxplot(column="Height (m)", \ xlabel="Meters", vert=False, figsize=(15, 3)) h_quantiles = numpy.quantile(pokemon_data["Height (m)"], \ numpy.array([0.00, 0.25, 0.50, 0.75, 1.00])) height_plot.vlines(h_quantiles, [0] * h_quantiles.size, [1] * h_quantiles.size, \ color='b', ls=':', lw=0.5, zorder=0) height_plot.set_ylim(0.5, 1.5) height_plot.set_xlim(-1.0, 21) height_plot.set_xticks([2.5, 5.0, 7.5, 10.0, 12.5, 15.0, 17.5] + h_quantiles.tolist()) height_plot
<Axes: xlabel='Meters'>
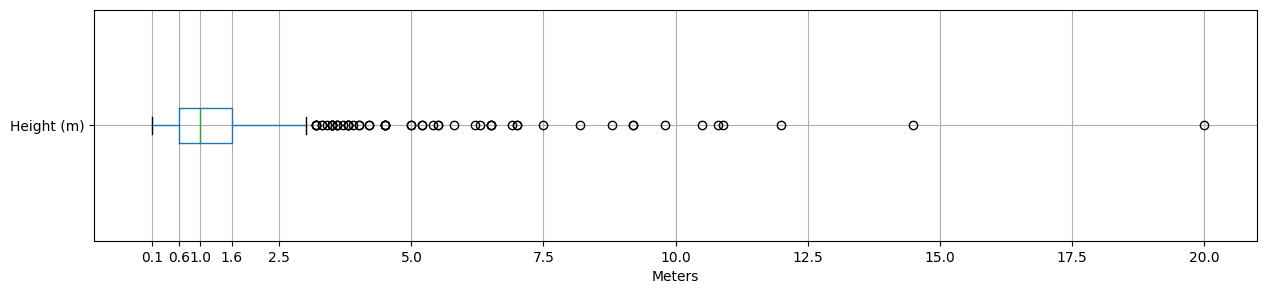
As you can just about see, the median height of a Pokémon is 1.0m (3'3"), which is about as tall as a guitar is long. The smallest Pokémon is 0.1m (0'4") tall - about the size of a credit card. Unsuprisingly the 8 Pokémon that are this size comprise a bug type, a handful of ghost types and fairy types, and a literal god. The largest Pokémon, Eternatus is not quite a god, but gets close, and is also capable of growing to 100m (328'1") during the course of Pokémon Sword and Shield's story. For reference, 20m is about the size of a tennis court, whilst 100m is about the height of Elizabeth Tower - the clock tower famous for housing Big Ben in London.
Focusing on the statistics, whilst there is a wide range of Pokémon heights, most are between 0.6m (2'0") and 1.6m (5'3"), with the highest concentration between 0.6m and 1.0m. This suggests that, whilst a player's starting guess in Squirdle should be 1.0m, their second guess should be in the range of 0.6m and 1.6m, unless they got it right first time.
I think I should mention at this point that - whilst these seem like huge data sets that will require wild amounts of luck to navigate - when combined with the type information we have gathered, height and weight become much easier to estimate.
What is the weight distribution?
Now that we have identified the average generation, type, and height (Generation V, water type, 1.0m), I will turn my attention to weight. Using the same boxplot method as I did in height, we can find the average weight. Similarly to the height section, all analysis will be done in metric units and later converted to imperial.
weight_plot = pokemon_data.boxplot(column="Weight (kgs)", \ xlabel="Kilograms", vert=False, figsize=(15, 3)) w_quantiles = numpy.quantile(pokemon_data["Weight (kgs)"], \ numpy.array([0.00, 0.25, 0.50, 0.75, 1.00])) weight_plot.vlines(w_quantiles, [0] * w_quantiles.size, [1] * w_quantiles.size, \ color='b', ls=':', lw=0.5, zorder=0) weight_plot.set_ylim(0.5, 1.5) weight_plot.set_xlim(-10.0, 1010.0) weight_plot.set_xticks([200, 400, 600, 800] + w_quantiles.tolist()) weight_plot
<Axes: xlabel='Kilograms'>
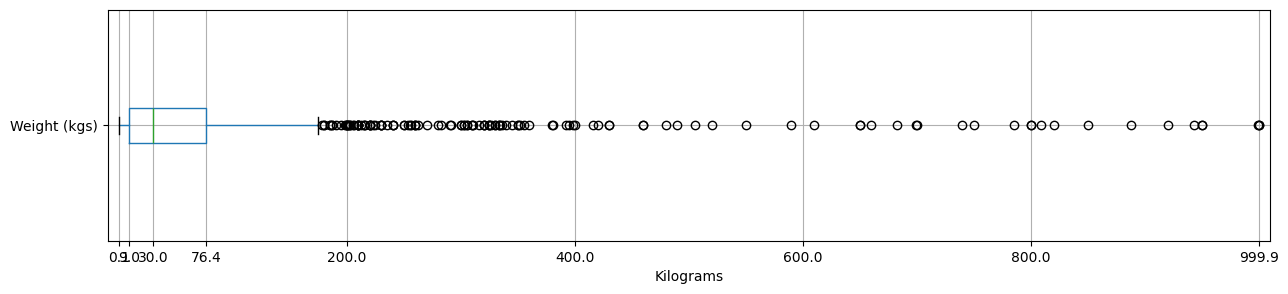
This boxplot isn't very useful: It's far too zoomed out, but we can see that the heaviest Pokémon is 999.9kg (2204.4lbs). There are two Pokémon that hold this rank: Cosmoem, the same god that was mentioned in the shortest Pokémon discussion, and Celesteela, a living bell from another dimension. For reference, 1000kg is the rough weight of a saltwater crocodile or the Liberty Bell.
weight_plot_z = pokemon_data.boxplot(column="Weight (kgs)", \ xlabel="Kilograms", vert=False, figsize=(15, 3)) weight_plot_z.vlines(w_quantiles, [0] * w_quantiles.size, \ [1] * w_quantiles.size, color='b', ls=':', lw=0.5, zorder=0) weight_plot_z.set_ylim(0.5, 1.5) weight_plot_z.set_xlim(-10.0, 210.0) weight_plot_z.set_xticks([200] + w_quantiles.tolist()[:-1]) weight_plot_z
<Axes: xlabel='Kilograms'>
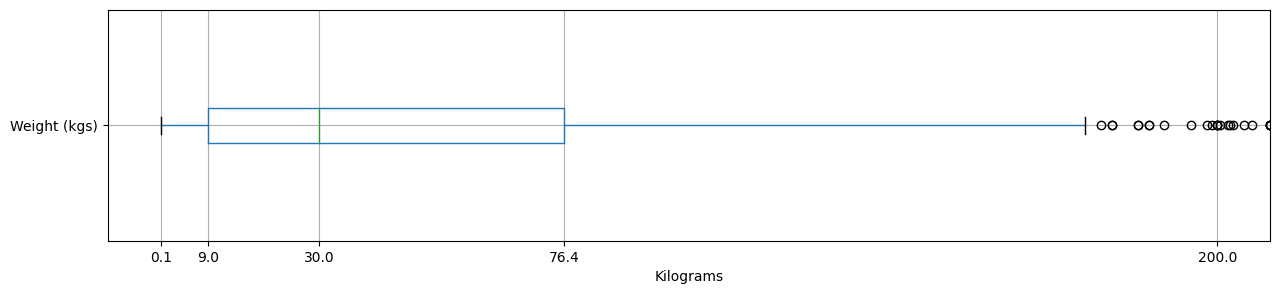
Now that we can get a closer look at the light Pokémon, we can see that the median weight is 30.0kg (66.1lbs), whilst the lighest is 0.1kg (0.2lbs). Again, despite the wide range of possible weights, the highest concentration of Pokémon lies between 0.1kg and 9.0kg (19.8lbs). Applying the same analysis to weight as we did height, I would suggest that a Squirdle's first guess should be around 30.0kg, whilst the second should be between 9.0kg and 76.4kg (168.7lbs).
For context, 30.0kg is around the weight of a garden bench, 0.1kg is around the weight of a mouse, 9.0kg is on par with an office chair, and 76.4kg is the weight of a washing machine. If you have ever moved a washing machine, you know the pain.
Discussion
We now have all the details of our average Pokémon: Generation V, water type, 1.0m, 30.0kg. So now we must consider the most cruical question of all: What does our average Pokémon look like? Previously I mentioned that there are 17 Generation V Pokémon that meet the type criteria. Let's meet the crew.
dex_nums = [501, 502, 503, 515, 516, 535, 536, \ 537, 550, 564, 565, 580, 581, 592, 593, 594, 647] front_runners = pokemon_data.loc[pokemon_data['#'].isin(dex_nums)] front_runners
| Index | # | Name | Type | Height (ft) | Height (m) | Weight (lbs) | Weight (kgs) | BMI |
|---|---|---|---|---|---|---|---|---|
| 613 | 501 | Oshawott | Water | 1′08″ | 0.5 | 13.0 | 5.9 | 23.6 |
| 614 | 502 | Dewott | Water | 2′07″ | 0.8 | 54.0 | 24.5 | 38.3 |
| 615 | 503 | Samurott | Water | 4′11″ | 1.5 | 208.6 | 94.6 | 42.0 |
| 616 | 503 | Samurott\nHisuian Samurott | Water\nDark | 4′11″ | 1.5 | 128.3 | 58.2 | 25.9 |
| 628 | 515 | Panpour | Water | 2′00″ | 0.6 | 29.8 | 13.5 | 37.5 |
| 629 | 516 | Simipour | Water | 3′03″ | 1.0 | 63.9 | 29.0 | 29.0 |
| 649 | 535 | Tympole | Water | 1′08″ | 0.5 | 9.9 | 4.5 | 18.0 |
| 650 | 536 | Palpitoad | Water\nGround | 2′07″ | 0.8 | 37.5 | 17.0 | 26.6 |
| 651 | 537 | Seismitoad | Water\nGround | 4′11″ | 1.5 | 136.7 | 62.0 | 27.6 |
| 665 | 550 | Basculin\nRed-Striped Form | Water | 3′03″ | 1.0 | 39.7 | 18.0 | 18.0 |
| 666 | 550 | Basculin\nBlue-Striped Form | Water | 3′03″ | 1.0 | 39.7 | 18.0 | 18.0 |
| 667 | 550 | Basculin\nWhite-Striped Form | Water | 3′03″ | 1.0 | 39.7 | 18.0 | 18.0 |
| 686 | 564 | Tirtouga | Water\nRock | 2′04″ | 0.7 | 36.4 | 16.5 | 33.7 |
| 687 | 565 | Carracosta | Water\nRock | 3′11″ | 1.2 | 178.6 | 81.0 | 56.3 |
| 704 | 580 | Ducklett | Water\nFlying | 1′08″ | 0.5 | 12.1 | 5.5 | 22.0 |
| 705 | 581 | Swanna | Water\nFlying | 4′03″ | 1.3 | 53.4 | 24.2 | 14.3 |
| 716 | 592 | Frillish | Water\nGhost | 3′11″ | 1.2 | 72.8 | 33.0 | 22.9 |
| 717 | 593 | Jellicent | Water\nGhost | 7′03″ | 2.2 | 297.6 | 135.0 | 27.9 |
| 718 | 594 | Alomomola | Water | 3′11″ | 1.2 | 69.7 | 31.6 | 21.9 |
| 778 | 647 | Keldeo\nOrdinary Form | Water\nFighting | 4′07″ | 1.4 | 106.9 | 48.5 | 24.7 |
| 779 | 647 | Keldeo\nResolute Form | Water\nFighting | 4′07″ | 1.4 | 106.9 | 48.5 | 24.7 |
These are our final contestants for the coveted role of first guess on Squirdle. How do we narrow it down from here? The next step is to normalise the data. We know the median height (1.0m) and weight (30.0kg), meaning we can express the heights and weights of these Pokémon as a distance from those medians. In other words, we are going to subtract the median height and weight from the height and weight of each of these Pokémon.
stripped = front_runners.loc[front_runners['#'].isin(dex_nums),\ ["Name", "Height (m)", "Weight (kgs)"]] stripped["Height (m)"] = stripped["Height (m)"] - 1.0 stripped["Weight (kgs)"] = stripped["Weight (kgs)"] - 30.0 stripped["Absolute Height"] = stripped["Height (m)"].abs() stripped["Absolute Weight"] = stripped["Weight (kgs)"].abs() stripped.sort_values(by=["Absolute Height", "Absolute Weight"])
| # | Name | Height (m) | Weight (kgs) | Absolute Height | Absolute Weight |
|---|---|---|---|---|---|
| 629 | Simipour | 0.0 | -1.0 | 0.0 | 1.0 |
| 665 | Basculin\nRed-Striped Form | 0.0 | -12.0 | 0.0 | 12.0 |
| 666 | Basculin\nBlue-Striped Form | 0.0 | -12.0 | 0.0 | 12.0 |
| 667 | Basculin\nWhite-Striped Form | 0.0 | -12.0 | 0.0 | 12.0 |
| 718 | Alomomola | 0.2 | 1.6 | 0.2 | 1.6 |
| 716 | Frillish | 0.2 | 3.0 | 0.2 | 3.0 |
| 614 | Dewott | -0.2 | -5.5 | 0.2 | 5.5 |
| 650 | Palpitoad | -0.2 | -13.0 | 0.2 | 13.0 |
| 687 | Carracosta | 0.2 | 51.0 | 0.2 | 51.0 |
| 705 | Swanna | 0.3 | -5.8 | 0.3 | 5.8 |
| 686 | Tirtouga | -0.3 | -13.5 | 0.3 | 13.5 |
| 778 | Keldeo\nOrdinary Form | 0.4 | 18.5 | 0.4 | 18.5 |
| 779 | Keldeo\nResolute Form | 0.4 | 18.5 | 0.4 | 18.5 |
| 628 | Panpour | -0.4 | -16.5 | 0.4 | 16.5 |
| 613 | Oshawott | -0.5 | -24.1 | 0.5 | 24.1 |
| 704 | Ducklett | -0.5 | -24.5 | 0.5 | 24.5 |
| 649 | Tympole | -0.5 | -25.5 | 0.5 | 25.5 |
| 616 | Samurott\nHisuian Samurott | 0.5 | 28.2 | 0.5 | 28.2 |
| 651 | Seismitoad | 0.5 | 32.0 | 0.5 | 32.0 |
| 615 | Samurott | 0.5 | 64.6 | 0.5 | 64.6 |
| 717 | Jellicent | 1.2 | 105.0 | 1.2 | 105.0 |
pokemon_data.loc[pokemon_data['#'] == 516]
| Index | # | Name | Type | Height (ft) | Height (m) | Weight (lbs) | Weight (kgs) | BMI |
|---|---|---|---|---|---|---|---|---|
| 629 | 516 | Simipour | Water | 3′03″ | 1.0 | 63.9 | 29.0 | 29.0 |
Having normalised the data and sorted it by how close it is to the median values, we can see that our most average Pokémon is #516 Simipour! As a mono water type it not only meets our criteria for being in the most popular type group, but also helps to determine if the Pokémon we are looking for is in the 45% of Pokémon that only have a single type. Simipour is exactly 1.0m tall, and weighing in at 29.0kg (63.9lbs) it is only 1kg short of the median.
Conclusion
Through this investigation I discovered the most average Pokémon. Why? Why take the time to do this? Put simply, I love Pokémon, and enjoy playing Squirdle every day. But also I think it is very important to show how data can be used and how powerful it is for making decisions. There are issues with bias in data, not only in its generation but also the decision-making process after the data has been consulted. Bureaucracy thrives on data and the security it gives. It gives the people making decisions an out, something to point to when things go wrong. "The data said this animal is dangerous, so we put them all down. It's not our fault that thousands of people are now upset." Or "the data says people from this area aren't very smart, so we'll give students a lower grade. Oh look, they got bad grades!"
Data ignores the context. Information includes it. Knowledge learns from it.
Why was I more inclined to guess Prinplup first over a later Pokémon? Was it that Piplup was my first starter Pokémon? Was it that Simipour has a forgettable design? Do I prefer penguins to monkeys? Is the animal violent, or are they raised by violent people? Are the students not very smart, or are they used to low expectations in difficult surroundings?
Dig into your data and learn from the why, rather than depending on the what.